Estimation
Propagation
Continous time
Higher relative degree
Towards safe robots that learn
Vikas Dhiman
Postdoc at UCSD
Postdoc at UCSD
Success of Reinforcement Learning

We want autonomous cars
Google trends for 'Autonomous cars'
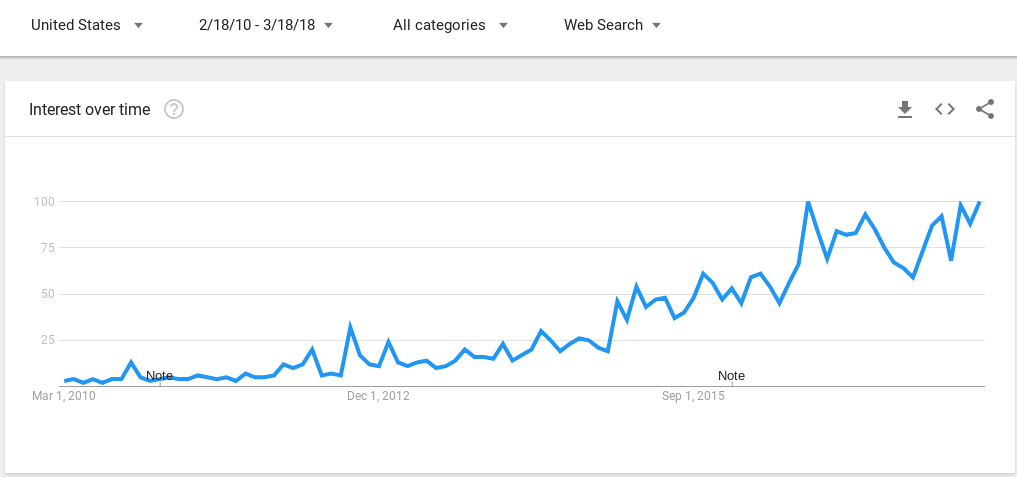









Why?


Big Data is not enough.
Data brings uncertainity.
How to handle uncertainity safely?
My Background
Today's focus

Given:
- Map and localization (Full observability)
- Desired trajectory as a plan
- Unsafe regions
Unknown (to learn from samples):
- Robot system dynamics
Want:
- Follow trajectory avoiding unsafe actions
Problem formulation

- \begin{align} \label{eq:system_dyanmics} \dot{\bfx} = f(\bfx) + g(\bfx)\bfu = \begin{bmatrix} f(\bfx) & g(\bfx)\end{bmatrix} \begin{bmatrix}1\\\bfu\end{bmatrix} =: F(\bfx) \ctrlaff \end{align}
- \[ \vect(F(\bfx)) \sim \GP(\vect(\bfM_0(.)), \bfK_0(.,.)) \]
-
\begin{align} \min_{\bfu_k \in \mathcal{U}}& \text{ Task cost function } \\ \qquad\text{s.t.}&~~\bbP\bigl( \text{ Safety constraint } \mid \bfx_k,\bfu_k \bigr) \ge \tilde{p}_k, \end{align}\begin{align} \min_{\bfu_k \in \mathcal{U}}& \|\bfu_k - \cssId{highlight-border-red-1}{\class{fragment}{\pi_\epsilon(\bfx_k)}} \|_Q \\ \qquad\text{s.t.}&~~\bbP\bigl( \cssId{highlight-border-red-1}{\class{fragment}{h(\bfx) > \zeta_h > 0}} \mid \bfx_k,\bfu_k \bigr) \ge \tilde{p}_k, \end{align}
Approach
- Estimate \(F(\bfx)\) with uncertainity.
- Propagate uncertainty to the Safety condition.
- Extension to continous time using Lipchitz continuity assumptions.
- Extension to higher relative degree systems.
Matrix Variate Gaussian Processes
\[
\vect(F(\bfx)) \sim \GP(\vect(\bfM_0(.)), \bfK_0(.,.))
\]
Option 1: Learn each matrix element independently
\[
\bfK_0(\bfx, \bfx')_{i, j} = \kappa(\bfx, \bfx')
\]
No correlation across dimensions
Option 2: Alvarez et al (FTML 2012):
\[
\bfK_0(\bfx, \bfx') = \kappa(\bfx, \bfx') \boldsymbol{\Sigma}
\]
\(\Sigma \in \R^{n(1+m) \times (1+m)n}\) has too many parameters to learn
Option 3: Sun et al (AISTATS 2017)
\[
F \sim \mathcal{MVG}(\bfM, \bfA, \bfB) \Leftrightarrow
\vect(F) \sim \calN(\vect(M), \bfB \otimes \bfA)
\]
\[
\bfK_0(\bfx, \bfx') = \bfB_0(\bfx, \bfx') \otimes \bfA
\]
Factorization assumption:
\[
\vect(F(\bfx)) \sim \GP(\vect(\bfM_0(.)), \bfB_0(.,.) \otimes \bfA)
\]
Matrix variate Gaussian Process
\(
\newcommand{\prl}[1]{\left(#1\right)}
\newcommand{\brl}[1]{\left[#1\right]}
\newcommand{\crl}[1]{\left\{#1\right\}}
\)
\begin{equation}
\begin{aligned}
\vect(F(\bfx)) &\sim \mathcal{GP}(\vect(\bfM_0(\bfx)), \bfB_0(\bfx,\bfx') \otimes \bfA)
%F(\bfx)\underline{\bfu} &\sim \mathcal{GP}(\bfM_0(\bfx)\underline{\bfu}, \underline{\bfu}^\top \bfB_0(\bfx,\bfx') \underline{\bfu}' \otimes \bfA)
\end{aligned}
\end{equation}
Given data \(\StDat_{1:k} := [\bfx(t_1), \dots, \bfx(t_k)]\),
\(\StDtDat_{1:k}=[\dot{\bfx}(t_1), \dots, \dot{\bfx}(t_k)] \),
and \( \underline{\boldsymbol{\mathcal{U}}}_{1:k}:= \diag(\ctrlaff_1, \dots, \ctrlaff_k) \).
\begin{equation*}
\begin{aligned}
\bfM_k(\bfx_*) &:= \bfM_0(\bfx_*) + \prl{ \dot{\bfX}_{1:k} - \boldsymbol{\mathcal{M}}_{1:k}\underline{\boldsymbol{\mathcal{U}}}_{1:k}} \prl{\underline{\boldsymbol{\mathcal{U}}}_{1:k}^\top\bfB_0(\bfX_{1:k},\bfX_{1:k})\underline{\boldsymbol{\mathcal{U}}}_{1:k}}^{-1}\underline{\boldsymbol{\mathcal{U}}}_{1:k}^\top\bfB_0(\bfX_{1:k},\bfx_*)\\
\bfB_k(\bfx_*,\bfx_*') &:= \bfB_0(\bfx_*,\bfx_*') + \bfB_0(\bfx_*,\bfX_{1:k})\underline{\boldsymbol{\mathcal{U}}}_{1:k}\prl{\underline{\boldsymbol{\mathcal{U}}}_{1:k}^\top\bfB_0(\bfX_{1:k},\bfX_{1:k})\underline{\boldsymbol{\mathcal{U}}}_{1:k}}^{-1}\underline{\boldsymbol{\mathcal{U}}}_{1:k}^\top\bfB_0(\bfX_{1:k},\bfx_*')
\label{eq:mvg-posterior}
\end{aligned}
\end{equation*}
Inference on MVGP:
\begin{align}
\vect(F_k(\bfx_*)) &\sim
\mathcal{GP}(\vect(\bfM_k(\bfx_*)), \; \bfB_k(\bfx_*,\bfx_*') \otimes \bfA).
\\
F_k(\bfx_*)\underline{\bfu}_* &\sim
\mathcal{GP}(\bfM_k(\bfx_*)\underline{\bfu}_*, \;
\underline{\bfu}_*^\top\bfB_k(\bfx_*,\bfx_*')\underline{\bfu}_*\otimes\bfA).
\end{align}
Approach
- Estimate \(F(\bfx)\) with Matrix-Variate Gaussian Process
- Propagate uncertainty to the Safety condition
- Extension to continous time using Lipchitz continuity assumptions.
- Extension to higher relative degree systems.
Control Barrier Functions

-
For differentiable \( h(\bfx) \),
safe set is \( \calC = \{ \bfx \in \calX : h(\bfx) > 0 \} \) - Assume \( \grad_\bfx h(\bfx) \ne 0 \quad \forall x \in \partial \calC \)
- Assume system starts in safe state \( \bfx(0) \in \calC \)
- Ames et al (ECC 2019): \begin{multline} \text{ System stays safe } \Leftrightarrow~~\exists~\bfu = \pi(\bfx)~~\text{s.t.}\\ \mbox{CBC}(\bfx,\bfu) := \Lie_f h(\bfx) + \Lie_g h(\bfx)\bfu + \alpha(h(\bfx)) \ge 0 \;~ \forall \bfx \in \calX. \end{multline} where \( \alpha(y) \) is some extended class \( \calK_\infty \) function
Uncertainity propagation to CBC
- \begin{align} \mbox{CBC}(\bfx, \bfu) &:= \Lie_{f}h(\bfx) + \Lie_{g}h(\bfx)\bfu + \alpha(h(\bfx)) \end{align}
- \[ \mbox{CBC}(\bfx, \bfu)= \grad_\bfx h(\bfx)F_k(\bfx)\ctrlaff + \alpha(h(\bfx)) \]
- Recall: \begin{equation} F_k(\bfx_*)\underline{\bfu}_* \sim \mathcal{GP}(\bfM_k(\bfx_*)\underline{\bfu}_*, \underline{\bfu}_*^\top\bfB_k(\bfx_*,\bfx_*')\underline{\bfu}_*\otimes\bfA). \end{equation}
- Lemma : \[ \mbox{CBC}(\bfx, \bfu) \sim \GP(\E[\mbox{CBC}], \Var(\mbox{CBC})) \] \begin{align} \label{eq:parametofpi5543} \E[\mbox{CBC}_k](\bfx, \bfu) &= \nabla_\bfx h(\bfx)^\top \bfM_k(\bfx)\underline{\bfu} + \alpha(h(\bfx)),\\ \Var[\mbox{CBC}_k](\bfx, \bfx'; \bfu) &= \underline{\bfu}^\top\bfB_k(\bfx,\bfx')\underline{\bfu} \nabla_\bfx h(\bfx)^{\top}\bfA\nabla_\bfx h(\bfx') \end{align} Note: mean and variance are Affine and Quadratic in \( \bfu \) respectively.
Deterministic condition for controller
-
\begin{align} \min_{\bfu_k \in \mathcal{U}}& \text{ Task cost function } \\ \qquad\text{s.t.}&~~\bbP\bigl( \text{ Safety constraint } \mid \bfx_k,\bfu_k \bigr) \ge \tilde{p}_k, \end{align}\begin{align} \min_{\bfu_k \in \mathcal{U}}& \|\bfu_k - \pi_\epsilon(\bfx_k) \|_Q \\ \qquad\text{s.t.}&~~\bbP\bigl( \style{color:red}{\mbox{CBC}(\bfx_k, \bfu_k) > \zeta > 0} \mid \bfx_k,\bfu_k \bigr) \ge \tilde{p}_k, \end{align}
- \[ \newcommand{\CBC}{\mbox{CBC}} \bbP\bigl(\mbox{CBC}(\bfx_k, \bfu_k) > \zeta \mid \bfx_k,\bfu_k \bigr) \ge \tilde{p}_k \\ \Leftrightarrow \frac{1}{2}-\frac{1}{2} \erf\left( \frac{\zeta - \E[\CBC] }{\sqrt{2\Var(\CBC)}} \right) \ge \tilde{p}_k \] where \( \erf(y) \) is there error function.
- Safe controller (an SOCP): \begin{align} \min_{\bfu_k \in \mathcal{U}}& \|\bfu_k - \pi_\epsilon(\bfx_k) \|_Q \\ \qquad\text{s.t.}\qquad& \cssId{highlight-current-red-1}{\class{fragment}{ \E[\CBC] - \zeta \ge \sqrt{2\Var(\CBC)(\erf^{-1}(1-2\tilde{p}_k))^2} }} \end{align}
Approach
- Estimate \(F(\bfx)\) with Matrix-Variate Gaussian Process
- Propagate uncertainty to the Control Barrier condition.
- Extension to continous time using Lipchitz continuity assumptions.
- Extension to higher relative degree systems.
Safety beyond triggering times
- So far: \begin{align} \min_{\bfu_k \in \mathcal{U}}& \|\bfu_k - \pi_\epsilon(\bfx_k) \|_Q \\ \qquad\text{s.t.}&~~ \bbP\bigl( \mbox{CBC}(\style{color:red}{\bfx_k}, \bfu_k) > \style{color:red}{\zeta} \mid \bfx_k,\bfu_k \bigr) \ge \style{color:red}{\tilde{p}_k}, \end{align}
- Next: \begin{align} \min_{\bfu_k \in \mathcal{U}}& \|\bfu_k - \pi_\epsilon(\bfx_k) \|_Q \\ \qquad\text{s.t.}&~~ \bbP\bigl( \mbox{CBC}(\style{color:red}{\bfx(t)}, \bfu_k) > \style{color:red}{0} \mid \bfx_k,\bfu_k \bigr) \ge \style{color:red}{p_k}, \qquad \style{color:red}{\forall t \in [t_k, \tau_k)} \end{align}
Safety beyond triggering times
- Assume Lipchitz continuity of dynamics: \begin{align} \textstyle \label{eq:smoth23} \bbP\left( \sup_{s \in [0, \tau_k)}\|F(\bfx(t_k+s))\ctrlaff_k -F(\bfx(t_k))\ctrlaff_k\| \le L_k \|\bfx(t_k+s)-\bfx_k\| \right) \ge q_k:=1-e^{-b_kL_k}. \end{align}
- Assume Lipchitz continuity of \( \alpha(h(\bfx)) \): \begin{align} \label{htym6!7uytf} |\alpha \circ h(\bfx(t_k+s))-\alpha \circ h(\bfx_k)| \le L_{\alpha \circ h} \|\bfx(t_k+s)-\bfx_k\|. \end{align}
Theorem:
\[
\bbP\bigl(
\mbox{CBC}(\bfx_k, \bfu_k) > \zeta
\mid \bfx_k,\bfu_k
\bigr) \ge \tilde{p}_k
\quad\Rightarrow\quad
\bbP\bigl(
\mbox{CBC}(\bfx(t), \bfu_k) > 0
\mid \bfx_k,\bfu_k
\bigr) \ge p_k, \;
\forall t \in [t_k, \tau_k)
\]
holds with \( p_k = \tilde{p}_k q_k \) and
\(
\tau_k \le \frac{1}{L_k}\ln\left(1+\frac{L_k\zeta}{(\chi_kL_k+L_{\alpha \circ h})\|\dot{\bfx}_k\|}\right)
\)
Approach
- Estimate \(F(\bfx)\) with Matrix-Variate Gaussian Process
- Propagate uncertainty to the Control Barrier condition.
- Extension to continous time using Lipchitz continuity assumptions.
- Extension to higher relative degree systems.
Higher relative degree CBFs
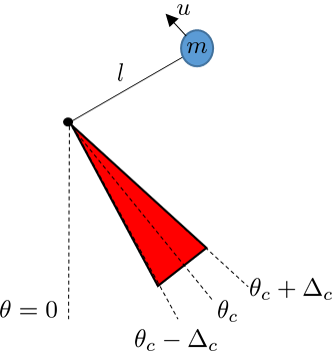
- \begin{align} \begin{bmatrix} \dot{\theta} \\ \dot{\omega} \end{bmatrix} = \underbrace{\begin{bmatrix} \omega \\ -\frac{g}{l} \sin(\theta) \end{bmatrix}}_{f(\bfx)} + \underbrace{\begin{bmatrix} 0 \\ \frac{1}{ml} \end{bmatrix}}_{g(\bfx)} u \end{align}
- \begin{align} h\left(\begin{bmatrix} \theta \\ \omega \end{bmatrix} \right) = \cos(\Delta_{col}) - \cos(\theta - \theta_c) \end{align}
- Note that \( \Lie_g h(\bfx) = \grad h(\bfx) g(\bfx) = 0 \)
- Thus \( \CBC(\bfx, \bfu) \) is independent of u.
Exponential Control Barrier Functions (ECBF)
- \[ \CBCr(\bfx, \bfu) := \Lie_f^{(r)} h(\bfx) + \Lie_g \Lie_f^{(r-1)} h(\bfx) \bfu + K_\alpha \begin{bmatrix} h(\bfx) \\ \Lie_f h(\bfx) \\ \vdots \\ \Lie_f^{(r-1)} h(\bfx) \end{bmatrix} \]
- \( r \ge 1 \) is the relative degree of CBF, \( h(\bfx) \), then \( \Lie_g \Lie_f^{k} h(\bfx) = 0, \; \forall k = \{0, \dots, r-2 \} \) and \( \Lie_g \Lie_f^{(r-1)} h(\bfx) \ne 0 \) and
Propagating uncertainity to \( \CBCtwo \)
- \[ \CBCtwo(\bfx, \bfu) = [\grad_\bfx \Lie_f h(\bfx)]^\top F(\bfx)\ctrlaff + K_\alpha \begin{bmatrix} h(\bfx) & \Lie_f h(\bfx) \end{bmatrix}^\top \]
- \( \Lie_f h(\bfx) = \grad_x h(\bfx) f(\bfx) \) is a Gaussian process
-
\( \grad_\bfx \Lie_f h(\bfx) \) is a Gaussian process
-
If \( p(\bfx) \sim \GP(\mu(\bfx), \kappa(\bfx, \bfx'))\), then
\( \grad_\bfx p(\bfx) \sim \GP(\grad_\bfx \mu(\bfx), H_\bfx \kappa(\bfx, \bfx')) \)
-
If \( p(\bfx) \sim \GP(\mu(\bfx), \kappa(\bfx, \bfx'))\), then
Propagating uncertainity to \( \CBCtwo \)
- \[ \CBCtwo(\bfx, \bfu) = [\grad_\bfx \Lie_f h(\bfx)]^\top F(\bfx)\ctrlaff + K_\alpha \begin{bmatrix} h(\bfx) & \Lie_f h(\bfx) \end{bmatrix}^\top \]
- \( \Lie_f h(\bfx) = \grad_x h(\bfx) f(\bfx) \) is a Gaussian process
- \( \grad_\bfx \Lie_f h(\bfx) \) is a Gaussian process
-
\( [\grad_\bfx \Lie_f h(\bfx)]^\top F(\bfx)\ctrlaff \) is a quadratic form of GP (not a GP )
-
\(\newcommand{\trc}{\text{tr}}\)
If \(p(\bfx)\) and \(q(\bfy)\) are GPs then \(p(\bfx)^\top q(\bfx)\) is also a GP
\begin{multline} p(\bfx)^\top q(\bfx) \sim \GP(\mu_p(\bfx)^\top \mu_q(\bfx) + \trc(\Cov_{p,q}(\bfx, \bfx)), \\ 2\trc(\Cov_{p,q}(\bfx, \bfx'))^2 ) + p(\bfx)^\top \kappa_q(\bfx, \bfx') p(\bfx') \\ + q(\bfx)^\top \kappa_p(\bfx, \bfx') q(\bfx') + 2 q(\bfx)^\top \Cov_{p,q}(\bfx, \bfx') p(\bfx') \end{multline}
-
\(\newcommand{\trc}{\text{tr}}\)
If \(p(\bfx)\) and \(q(\bfy)\) are GPs then \(p(\bfx)^\top q(\bfx)\) is also a GP
-
\( \CBCtwo(\bfx, \bfu) \) is a quadratic form of GP.
\( \E[\CBCtwo](\bfx, \bfu) \) is still affine in \( \bfu \).
\( \Var[\CBCtwo](\bfx, \bfx'; \bfu) \) is still quadratic in \( \bfu \).
Extending to \(\CBCr\)
- \[ \CBCr(\bfx, \bfu) = [\grad_\bfx \Lie_f^{(r)} h(\bfx)]^\top F(\bfx)\ctrlaff + K_\alpha \begin{bmatrix} h(\bfx) & \Lie_f h(\bfx) & \dots \Lie_f^{(r-1)} h(\bfx) \end{bmatrix}^\top \]
-
-
\( \CBCr(\bfx, \bfu) \) is not a GP
\( \E[\CBCr](\bfx, \bfu) \) is still affine in \( \bfu \).
\( \Var[\CBCr](\bfx, \bfx'; \bfu) \) is still quadratic in \( \bfu \). - For \( r \ge 3 \), \(\CBCr\) statistics can be estimated by Monte-carlo methods.
Safe controller using ECBF
- \begin{align} \min_{\bfu_k \in \mathcal{U}}& \|\bfu_k - \pi_\epsilon(\bfx_k) \|_Q \\ \qquad\text{s.t.}&~~ \bbP\bigl( \CBCr(\bfx_k, \bfu_k) > \zeta \mid \bfx_k,\bfu_k \bigr) \ge \tilde{p}_k \end{align}
- Using Cantelli's (Chebyshev's one-sided) inequality
- Safe controller (an SOCP) \begin{align} \min_{\bfu_k \in \mathcal{U}}& \|\bfu_k - \pi_\epsilon(\bfx_k) \|_Q \\ \qquad\text{s.t.}\qquad &\E[\mbox{CBC}_k^{(r)}]-\zeta \ge \sqrt{\frac{\tilde{p}_k}{1-\tilde{p}_k}\Var[\mbox{CBC}_k^{(r)}]} \end{align}
Learning Experiments

- \begin{align} \begin{bmatrix} \dot{\theta} \\ \dot{\omega} \end{bmatrix} = \underbrace{\begin{bmatrix} \omega \\ -\frac{g}{l} \sin(\theta) \end{bmatrix}}_{f(\bfx)} + \underbrace{\begin{bmatrix} 0 \\ \frac{1}{ml} \end{bmatrix}}_{g(\bfx)} u \end{align}
- \begin{align} h\left(\begin{bmatrix} \theta \\ \omega \end{bmatrix} \right) = \cos(\Delta_{col}) - \cos(\theta - \theta_c) \end{align}
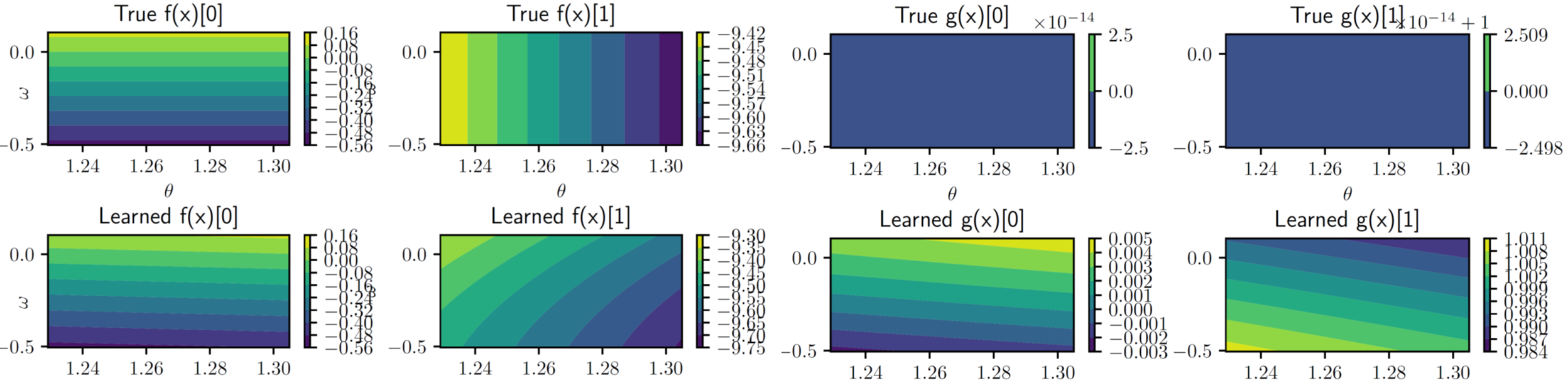
Safe controller using ECBF Experiments

- \begin{align} \begin{bmatrix} \dot{\theta} \\ \dot{\omega} \end{bmatrix} = \underbrace{\begin{bmatrix} \omega \\ -\frac{g}{l} \sin(\theta) \end{bmatrix}}_{f(\bfx)} + \underbrace{\begin{bmatrix} 0 \\ \frac{1}{ml} \end{bmatrix}}_{g(\bfx)} u \end{align}
- \begin{align} h\left(\begin{bmatrix} \theta \\ \omega \end{bmatrix} \right) = \cos(\Delta_{col}) - \cos(\theta - \theta_c) \end{align}

Take away
- Safety guarantees in stochastic control-affine systems were formuated as Quadratic contraints on the control signal using Exponential Control Barrier Functions.
Ongoing work
- More experiments (closer to the Motivation).
- Entropy objective to pick optimal actions for reducing uncertainity.
- Application of Hansen-Wright like inequalities for tighter bounds on \( \CBCr \)
- Shengyang Sun, Changyou Chen, and Lawrence Carin. Learning Structured Weight Uncertainty in Bayesian Neural Networks. In International Conference on Artificial Intelligence and Statistics (AISTATS), pages 1283–1292, 2017.
- A. D. Ames, S. Coogan, M. Egerstedt, G. Notomista, K. Sreenath, and P. Tabuada. Control barrier functions: Theory and applications. In 2019 18th European Control Conference (ECC), pages 3420–3431, June 2019. doi: 10.23919/ECC.2019.8796030.
- Mauricio A Alvarez, Lorenzo Rosasco, and Neil D Lawrence. Kernels for vector-valued functions: A review. Foundations and Trends in Machine Learning, 4(3):195–266, 2012.
- Niranjan Srinivas, Andreas Krause, Sham M Kakade, and Matthias Seeger. Gaussian process opti- mization in the bandit setting: No regret and experimental design. arXiv preprint arXiv:0912.3995, 2009.
- Quan Nguyen and Koushil Sreenath. Exponential control barrier functions for enforcing high relative- degree safety-critical constraints. In 2016 American Control Conference (ACC), pages 322–328. IEEE, 2016a.
- Louizos, Christos, and Max Welling. "Structured and efficient variational deep learning with matrix gaussian posteriors." International Conference on Machine Learning. 2016.
- Khojasteh, M. J., Dhiman, V., Franceschetti, M., & Atanasov, N. (2020). Probabilistic safety constraints for learned high relative degree system dynamics. L4DC 2020. available https://arXiv.org/abs/1912.10116.
- Learning from Interventions using Hierarchical Policies for Safe Learning J Bi, V Dhiman, T Xiao, C Xu - AAAI 2020. Available https://arXiv.org/abs/1912.02241
- Learning Navigation Costs from Demonstration in Partially Observable Environments T Wang, V Dhiman, N Atanasov. ICRA 2020. Available https://arXiv.org/abs/2002.11637
- Andrychowicz, Marcin, et al. "Hindsight experience replay." Advances in Neural Information Processing Systems. 2017.
- Mutual localization: Two camera relative 6-dof pose estimation from reciprocal fiducial observation. V Dhiman, J Ryde, JJ Corso. IROS 2013
- Learning Compositional Sparse Models of Bimodal Percepts. S Kumar, V Dhiman, JJ Corso AAAI, 2014
- Voxel planes: Rapid visualization and meshification of point cloud ensembles. J Ryde, V Dhiman, R Platt IROS, 2013
- Modern MAP inference methods for accurate and fast occupancy grid mapping on higher order factor graphs. V Dhiman, A Kundu, F Dellaert, JJ Corso ICRA 2014
- Continuous occlusion models for road scene understanding M Chandraker, V Dhiman. US Patent 9,821,813, 2017
- A continuous occlusion model for road scene understanding V Dhiman, QH Tran, JJ Corso, M Chandraker. CVPR 2016
- A Critical Investigation of DRL for Navigation V Dhiman, S Banerjee, B Griffin, JM Siskind, JJ Corso NeurIPS DRL Workshop, 2017.
- Learning Compositional Sparse Bimodal Models S Kumar, V Dhiman, PA Koch, JJ Corso. PAMI, 2017.
- (Mirowski et al. 2017) Learning to navigate in complex environments. In ICLR 2017.
- Multi-Goal Reinforcement Learning: Challenging Robotics Environments and Request for Research. Matthias Plappert and Marcin Andrychowicz and Alex Ray and Bob McGrew and Bowen Baker and Glenn Powell and Jonas Schneider and Josh Tobin and Maciek Chociej and Peter Welinder and Vikash Kumar and Wojciech Zaremba. ArXiV 2018. 1802.09464
- Kaelbling, Leslie Pack. "Learning to achieve goals." IJCAI. 1993.
- V. Dhiman, S. Banerjee, J. M. Siskind, and J. J. Corso. Learning goal-conditioned value functions with one-step path rewards rather than goal-rewards. In Submitted to ICLR, 2019. Under review.
- Zachariou, Peter et al. “SPEEDING Effects on hazard perception and reaction time.” (2011).
- Mnih, Volodymyr, et al. "Human-level control through deep reinforcement learning." Nature 518.7540 (2015): 529.
- Watkins, Christopher JCH, and Peter Dayan. "Q-learning." Machine learning 8.3-4 (1992): 279-292.
- Pearl, Judea. "Fusion, propagation, and structuring in belief networks." Artificial intelligence 29.3 (1986): 241-288.
- Jojic, Vladimir, Stephen Gould, and Daphne Koller. "Accelerated dual decomposition for MAP inference." ICML. 2010.
- Merali, Rehman S., and Timothy D. Barfoot. "Occupancy grid mapping with Markov chain monte carlo Gibbs sampling." Robotics and Automation (ICRA), 2013 IEEE International Conference on. IEEE, 2013.
- Shayle R Searle and Marvin HJ Gruber.Linear models. John Wiley & Sons, 1971
Bibliography
Thank you. Questions?
Paper URL: arxiv.org/abs/1912.10116
-
 Mohammad Javad Khojasteh\(^*\)
Mohammad Javad Khojasteh\(^*\)
[email protected]
http://www.its.caltech.edu/~mjkhojas/ -
 Vikas Dhiman\(^*\)
Vikas Dhiman\(^*\)
[email protected]
vikasdhiman.info -
 Massimo Franceschetti
Massimo Franceschetti
https://web.eng.ucsd.edu/~massimo/ -
 Nikolay Atanasov
Nikolay Atanasov
https://natanaso.github.io/


Probabilistic Safety Constraints:Vikas Dhiman