ECE 275: Representations of logic systems
Vikas Dhiman
[email protected]
TA: Pascal Francis-Mezger
[email protected]
Basic gates
AND gate
\( L_{\text{AND}}(x_1, x_2) = x_1 \cdot x_2 \)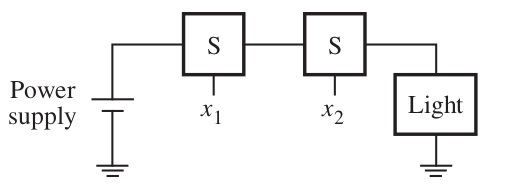
\( L_{\text{AND}}(x_1, x_2) = x_1 \cdot x_2 \)

OR gate
\( L_{\text{OR}}(x_1, x_2) = x_1 + x_2 \)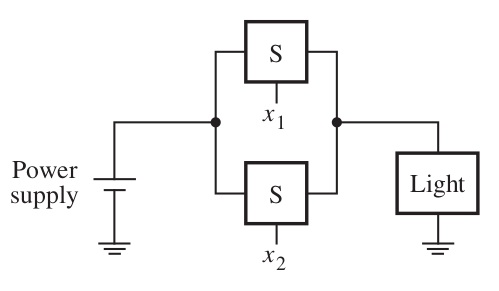
\( L_{\text{OR}}(x_1, x_2) = x_1 + x_2 \)

NOT gate
\( L_{\text{NOT}}(x_1) = \bar{x}_1 \)
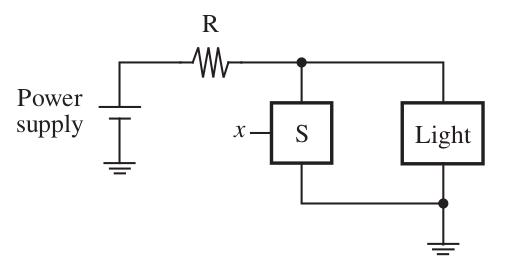
Source:Verilog 3rd, Brown and Vranesic 2014
\( L_{\text{NOT}}(x_1) = \bar{x}_1 \)

ANSI symbols
AND gate
\( L_{\text{AND}}(x_1, x_2) = x_1 \cdot x_2 \)
\( L_{\text{AND}}(x_1, x_2) = x_1 \cdot x_2 \)
OR gate
\( L_{\text{OR}}(x_1, x_2) = x_1 + x_2 \)
\( L_{\text{OR}}(x_1, x_2) = x_1 + x_2 \)
NOT gate
\( L_{\text{NOT}}(x_1) = \bar{x}_1 \)

\( L_{\text{NOT}}(x_1) = \bar{x}_1 \)
AND Gate
Circuit (an implentation)

Source:Verilog 3rd, Brown and Vranesic 2014

Source:Verilog 3rd, Brown and Vranesic 2014
Truth table
| Row num | \(x_1\) | \(x_2\) | \(x_1 \cdot x_2\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 |
Boolean expression
\(f = x_1 \cdot x_2 = x_1x_2\)
\(f = x_1 \cdot x_2 = x_1x_2\)
ANSI Symbol

OR Gate
Circuit (an implentation)

Source:Verilog 3rd, Brown and Vranesic 2014

Source:Verilog 3rd, Brown and Vranesic 2014
Truth table
| Row num | \(x_1\) | \(x_2\) | \(x_1 + x_2\) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 |
Boolean expression
\(f = x_1 + x_2 \)
\(f = x_1 + x_2 \)
ANSI Symbol

NOT Gate
Circuit (an implentation)

Source:Verilog 3rd, Brown and Vranesic 2014

Source:Verilog 3rd, Brown and Vranesic 2014
Truth table
| Row num | \(x_1\) | \(\bar{x}_1\) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Boolean expression
\(f = \bar{x}_1 \)
\(f = \bar{x}_1 \)
ANSI Symbol

Network to truth table
\( f = \overline{(A\bar{B} + C)} D \)
Truth table
| Row num | A | B | C | D | \(\bar{B}\) | g | h | k | f |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 13 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
Truth table to Minterms
Truth table
| Row num | A | B | C | D | f |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 |
Minterms
List of rows where function is 1
\(f = m_1 + m_5 + m_{13} \)
\(f = \sum m(1, 5, 13) \)
Minterms to Sum of products
Minterms
\(f = \sum m(1, 5, 13) \)
| \(m_0\) | \(\triangleq \bar{A} \bar{B} \bar{C} \bar{D} \) |
| \(m_1\) | \(\triangleq \bar{A} \bar{B} \bar{C} D \) |
| \(m_2\) | \(\triangleq \bar{A} \bar{B} C \bar{D} \) |
| \(m_3\) | \(\triangleq \bar{A} \bar{B} C D \) |
| \(m_4\) | \(\triangleq \bar{A} \bar{B} \bar{C} \bar{D} \) |
| \(m_5\) | \(\triangleq \bar{A} \bar{B} \bar{C} D \) |
| \(m_6\) | \(\triangleq \bar{A} \bar{B} C \bar{D} \) |
| \(m_7\) | \(\triangleq \bar{A} \bar{B} C D \) |
| \(m_8\) | \(\triangleq A \bar{B} \bar{C} \bar{D} \) |
| \(m_9\) | \(\triangleq A \bar{B} \bar{C} D \) |
| \(m_{10}\) | \(\triangleq A \bar{B} C \bar{D} \) |
| \(m_{11}\) | \(\triangleq A \bar{B} C D \) |
| \(m_{12}\) | \(\triangleq A B \bar{C} \bar{D} \) |
| \(m_{13}\) | \(\triangleq A B \bar{C} D \) |
| \(m_{14}\) | \(\triangleq A B C \bar{D} \) |
| \(m_{15}\) | \(\triangleq A B C D \) |
Sum of products
\(
f = \bar{A} \bar{B} \bar{C} D
+ \bar{A} \bar{B} \bar{C} D
+ A B \bar{C} D \)
Truth table to Maxterms
Truth table
| Row num | A | B | C | D | f |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 |
Maxterms
List of rows where function is 0
\[
f = M_0 \cdot M_2 \cdot M_3 \cdot M_4 \cdot M_6 \cdot M_7
\\
\cdot M_8 \cdot M_9 \cdot
M_{10} \cdot M_{11} \cdot M_{12} \cdot M_{14}
\\
\cdot M_{15}
\]
\(
f = \prod M(0, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 14, 15) \)
Maxterms to products of sums
Maxterms
\(f = \prod M(0, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 14, 15) \)
| \(M_0\) | \(\triangleq A + B + C + D \) |
| \(M_1\) | \(\triangleq A + B + C + \bar{D}\) |
| \(M_2\) | \(\triangleq A + B + \bar{C} + D \) |
| \(M_3\) | \(\triangleq A + B + \bar{C} + \bar{D}\) |
| \(M_4\) | \(\triangleq A + \bar{B} + C + D \) |
| \(M_5\) | \(\triangleq A + \bar{B} + C + \bar{D} \) |
| \(M_6\) | \(\triangleq A + \bar{B} + \bar{C} + D \) |
| \(M_7\) | \(\triangleq A + \bar{B} + \bar{C} + \bar{D}\) |
| \(M_8\) | \(\triangleq\bar{A} + B + \bar{C} + D \) |
| \(M_9\) | \(\triangleq\bar{A} + B + \bar{C} + \bar{D}\) |
| \(M_{10}\) | \(\triangleq\bar{A} + B + \bar{C} + D \) |
| \(M_{11}\) | \(\triangleq\bar{A} + B + \bar{C} + \bar{D}\) |
| \(M_{12}\) | \(\triangleq\bar{A} + \bar{B} + \bar{C} + D \) |
| \(M_{13}\) | \(\triangleq\bar{A} + \bar{B} + \bar{C} + \bar{D} \) |
| \(M_{14}\) | \(\triangleq\bar{A} + \bar{B} + \bar{C} + D \) |
| \(M_{15}\) | \(\triangleq\bar{A} + \bar{B} + \bar{C} + \bar{D}\) |
Products of sums
\begin{multline}
f = (A + B + C + D)( A + B + \bar{C} + D ) \dots
\\
(\bar{A} + \bar{B} + \bar{C} + D)
(\bar{A} + \bar{B} + \bar{C} + \bar{D})
\end{multline}
VENN Diagrams for gates
NOT Venn Diagram
\( f = \bar{x}_1 \); \(f = \bar{x}_2\)


\( f = \bar{x}_1 \); \(f = \bar{x}_2\)
AND Venn Diagram
\( f = x_1 \cdot x_2 \)

\( f = x_1 \cdot x_2 \)
OR Venn Diagram
\( f = x_1 + x_2 \)

\( f = x_1 + x_2 \)
Karnaugh maps for gates
AND K-map
\( f = x_1 \cdot x_2 \)
\( f = x_1 \cdot x_2 \)
| \(\bar{x}_1\) | \(x_1\) | |
|---|---|---|
| \(\bar{x}_2\) | 0 | 0 |
| \(x_2\) | 0 | 1 |
OR K-map
\( f = x_1 + x_2 \)
\( f = x_1 + x_2 \)
| \(\bar{x}_1\) | \(x_1\) | |
|---|---|---|
| \(\bar{x}_2\) | 0 | 1 |
| \(x_2\) | 1 | 1 |
NOT K-map
\( f = \bar{x}_1 \)
\( f = \bar{x}_1 \)
| \(\bar{x}_1\) | \(x_1\) |
|---|---|
| 1 | 0 |
Truth table to K-map
| Row num | A | B | C | D | f |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 |
K-map
| \(\bar{A}\) | \(A \) | ||||
|---|---|---|---|---|---|
| \(\bar{B}\) | \(B \) | \(\bar{B}\) | |||
| \(\bar{C}\) | \(\bar{D}\) | \(m_0\) | \(m_4\) | \(m_{12}\) | \(m_8\) |
| \(D\) | \(m_1\) | \(m_5\) | \(m_{13}\) | \(m_9\) | |
| \(C\) | \(m_3\) | \(m_7\) | \(m_{15}\) | \(m_{11}\) | |
| \(\bar{D}\) | \(m_2\) | \(m_6\) | \(m_{14}\) | \(m_{10}\) | |
Truth table to K-map
| Row num | A | B | C | D | f |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 |
K-map
| \(\bar{A}\) | \(A \) | ||||
|---|---|---|---|---|---|
| \(\bar{B}\) | \(B \) | \(\bar{B}\) | |||
| \(\bar{C}\) | \(\bar{D}\) | 0 | 0 | 0 | 0 |
| \(D\) | 1 | 1 | 1 | 0 | |
| \(C\) | 0 | 0 | 0 | 0 | |
| \(\bar{D}\) | 0 | 0 | 0 | 0 | |
K-map to expression
K-map
| \(\bar{A}\) | \(A \) | ||||
|---|---|---|---|---|---|
| \(\bar{B}\) | \(B \) | \(\bar{B}\) | |||
| \(\bar{C}\) | \(\bar{D}\) | 0 | 0 | 0 | 0 |
| \(D\) | 1 | 1 | 1 | 0 | |
| \(C\) | 0 | 0 | 0 | 0 | |
| \(\bar{D}\) | 0 | 0 | 0 | 0 | |
Expression
\(f = \bar{A}\bar{C}D + B\bar{C}D \)
Expression to truth table
Expression
\(f = \bar{A}\bar{C}D + B\bar{C}D \)Truth table
| Row num | A | B | C | D | \(\bar{A}\bar{C}D\) | \(B\bar{C}D\) | f |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Truth table to timing diagram
| Row num | A | B | C | D | f |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 |
Timing diagram
Truth table to timing diagram
| Row num | A | B | C | D | f |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 |