ECE 275: Boolean algebra

Vikas Dhiman
https://vikasdhiman.info/ECE275-Sequential-Logic/

On the naming of Mintems

The minterms and maxterms derive their names from the fact that they are respectively the minimum and maximum areas which may be defined on a Venn diagram .

NBS Technical Note. (1959)

\( m_0 = \bar{x}_1 \bar{x}_2 \)
\( m_1 = \bar{x}_1 x_2 \)
\( m_2 = x_1 \bar{x}_2 \)
\( m_3 = x_1 x_2 \)

Truth table to K-map

Row numABCDf
000000
100011
200100
300110
401000
501011
601100
701110
810000
910010
1010100
1110110
1211000
1311011
1411100
1511110

K-map

\(\bar{A}\) \(A \)
\(\bar{B}\) \(B \) \(\bar{B}\)
\(\bar{C}\)\(\bar{D}\) \(m_0\) \(m_4\) \(m_{12}\) \(m_8\)
\(D\) \(m_1\) \(m_5\) \(m_{13}\) \(m_9\)
\(C\) \(m_3\) \(m_7\) \(m_{15}\) \(m_{11}\)
\(\bar{D}\) \(m_2\) \(m_6\) \(m_{14}\) \(m_{10}\)
\(\bar{A}\) \(A \)
\(\bar{B}\) \(B \) \(\bar{B}\)
\(\bar{C}\)\(\bar{D}\) 0 0 0 0
\(D\) 1 1 1 0
\(C\) 0 0 0 0
\(\bar{D}\) 0 0 0 0

K-map to expression

K-map

\(\bar{A}\) \(A \)
\(\bar{B}\) \(B \) \(\bar{B}\)
\(\bar{C}\)\(\bar{D}\) 0 0 0 0
\(D\) 1 1 1 0
\(C\) 0 0 0 0
\(\bar{D}\) 0 0 0 0

Expression

\(f = \bar{A}\bar{C}D + B\bar{C}D \)

Expression to truth table

Expression

\(f = \bar{A}\bar{C}D + B\bar{C}D \)

Truth table

Row numABCD \(\bar{A}\bar{C}D\) \(B\bar{C}D\) f
0 0000000
1 0001101
2 0010000
3 0011000
4 0100000
5 0101111
6 0110000
7 0111000
8 1000000
9 1001000
101010000
111011000
121100000
131101011
141110000
151111000

Truth table to timing diagram

Row num0123456789101112131415
A0000000011111111
B0000111100001111
C0011001100110011
D0101010101010101
f0100010000000100

Boolean expression to Verilog

\( f = \overline{(A\bar{B} + C)}D \)

Verilog


module examplefunction1(A, B, C, D, f);
    input A, B, C, D;
    output f;
    assign f = (~(A&(~B) | C))&D;
endmodule

Functionally equiv networks

\(f_1 = \overline{(A\bar{B} + C)}D \)
\(f_2 = (\bar{A} + B)\bar{C}D \)

Boolean algebra

Axioms

  • \( 0 \cdot 0 = 0 \)
  • \( 1 + 1 = 1 \)
  • \( 1 \cdot 1 = 1 \)
  • \( 0 + 0 = 0 \)
  • \( 0 \cdot 1 = 1 \cdot 0 = 0 \)
  • \( \bar{0} = 1 \)
  • \( \bar{1} = 0 \)

Single variable Theorems

  • \( x \cdot 0 = 0 \)
  • \( x + 1 = 1 \)
  • \( x \cdot 1 = x \)
  • \( x + 0 = x \)
  • \( x \cdot x = x \)
  • \( x + x = x \)
  • \( x \cdot \bar{x} = 0 \)
    \( x + \bar{x} = 1 \)
  • \(\bar{\bar{x}} = x \)

Duality: Swap \( + \) with \( \cdot \) and \( 0 \) with \( 1 \) to get another law

Two and three variable properties

\(x \cdot y = y \cdot x\)Commutative
\(x + y = y + x\)
\(x \cdot (y \cdot z) = (x \cdot y) \cdot z\)Associative
\(x + (y + z)= (x + y) + z\)
\(x \cdot (y + z) = x\cdot y + x \cdot z\)Distributive
\(x + y\cdot z = (x+y) \cdot (x+z)\)

DeMorgan's theorem

  • \( \overline{x \cdot y} = \bar{x} + \bar{y} \)
  • \( \overline{x + y} = \bar{x} \cdot \bar{y} \)

DeMorgan's theorem

  • \( \overline{x \cdot y} = \bar{x} + \bar{y} \)
  • \( \overline{x + y} = \bar{x} \cdot \bar{y} \)

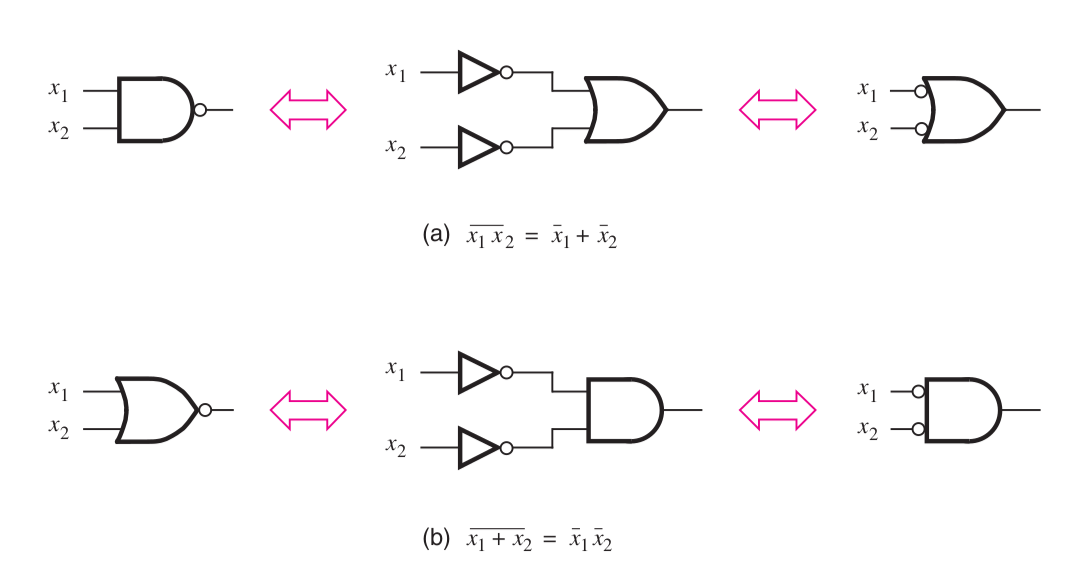
Prove that for two variable function

\( \bar{m}_0 = M_0 \)

Soln: Prove that for two variable function

\( \bar{m}_0 = M_0 \) \begin{align} m_0 &= \bar{x}_1 \bar{x}_2 & \text{ by definition of } m_0 \\ \implies \bar{m}_0 &= \overline{\bar{x}_1 \bar{x}_2} & \\ &= \bar{\bar{x}}_1 + \bar{\bar{x}}_2 & \text{ by DeMorgan's theorem } \\ &= x_1 + x_2 = M_0 & \text{ by definition of } M_0 \end{align}

Inequality

  • Define \(x \le y \) as \(x = 0\) whenever \( y = 0 \)
  • If \(x \le y \) and \( y \le x\), then \( x = y \)
  • If \(x \le y \), then \( x \cdot y = x \) and \(x + y = y\)
  • \(x \cdot z \le z \) and \( x \cdot z \le x\)

Two and three variable properties

\(x + x \cdot y = x \)Absorption
\(x \cdot (x + y) = x \)
\(x \cdot y + x \cdot \bar{y} = x \)Combining
\((x + y)\cdot (x + \bar{y}) = x \)

Two and three variable properties

\(x + \bar{x}y = x + y \)Concensus
\(x \cdot (\bar{x} + y) = x \cdot y \)
\(x \cdot y + y \cdot z + \bar{x} \cdot z = x \cdot y + \bar{x} \cdot z \)
\((x + y) \cdot ( y + z ) \cdot (\bar{x} + z) = (x + y) \cdot (\bar{x} + z) \)
\[ \newcommand{\bx}{\bar{x}} \newcommand{\by}{\bar{y}} \newcommand{\bz}{\bar{z}} \]

Prove that

If \( x + y = 1 \) and \( xy = 0 \) then \( \bx = y \)

Soln: Prove that

If \( x + y = 1 \) and \( xy = 0 \) then \( \bx = y \)
\begin{align} &x + y = 1 \\ &\implies x \bx + y \bx = \bx & \text{ multiply both sides by } \bx \\ &\implies y \bx = \bx & \because x \bx = 0 \\ &\implies y \bx + y x = \bx + y x & \text{ add } y x \text{ to both sides } \\ &\implies y (\bx + x) = \bx & \text{by dist. prop. and } xy = y x = 0 \\ &\implies y = \bx & \end{align}

Prove that for two variable function

\( \overline{\sum m(0, 2)} = \sum m(1, 3) \)

Soln: Prove that for two variable function

\( \overline{\sum m(0, 2)} = \sum m(1, 3) \)
We know that \( \sum m(0, 2) + \sum m(1, 3) = 1 \)
\begin{align} \left(\sum m(0, 2) \right)& \cdot \left(\sum m(1, 3) \right)\\ &= (\bx_1 \bx_2 + x_1 \bx_2)(\bx_1 x_2 + x_1 x_2) \\ &= \bx_1 \bx_2 \bx_1 x_2 + \bx_1 \bx_2 x_1 x_2 + x_1 \bx_2 \bx_1 x_2 + x_1 \bx_2 x_1 x_2 \\ &= 0 \end{align}

Prove that for three variable function

\( \sum m(0, 2, 3, 7) = \prod M(1, 4, 5, 6) \)

Soln: Prove that for three variable function

\begin{align} \sum m(0, 2, 3, 7) &= m_0 + m_2 + m_3 + m_7 \\ &= \overline{ m_1 + m_4 + m_5 + m_6} \\ &= \bar{m}_1 \bar{m}_4 \bar{m}_5 \bar{m}_6 \\ &= M_1 M_4 M_5 M_6 \\ &=\prod M(1, 4, 5, 6) \end{align}

Design of three-way light control

Soln: three-way light control


Truth table

Rowxyz f
0 0000
1 0011
2 0101
3 0110
4 1001
5 1010
6 1100
7 1111
\[ f = \sum m (1, 2, 4, 7) \\= \bar{x} \bar{y} z + \bar{x} y \bar{z} + x \bar{y} \bar{z} + xyz \]
\(\bar{x}\) \(x \)
\(\bar{y}\) \(y \) \(\bar{y}\)
\(\bar{z}\) 0 1 0 1
\(z\) 1 0 1 0

Design a multiplexer

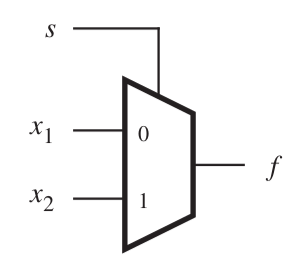
Soln: multiplexer

Rowsx_1x_2 f
0 0000
1 0010
2 0101
3 0111
4 1000
5 1011
6 1100
7 1111
\( f = \sum m(2, 3, 5, 7) \)
\(\bar{s}\) \(s \)
\(\bar{x_1}\) \(x_1 \) \(\bar{x_1}\)
\(\bar{x_2}\) 0 1 0 0
\(x_2\) 0 1 1 1

\(f = sx_1 + \bar{s} x_2 \)

Thanks, Questions, Feedback?

https://vikasdhiman.info/ECE275-Sequential-Logic/