Petrick's method

Hw2 Prob 8: POS form

$f (x_1 , x_2 , x_3 , x_4 ) = \sum m(0, 2, 8, 9, 12, 15) + D(1, 3, 6, 7).$

Alternative 5-var K-map

$F(A, B, C, D, E) = \sum m(0, 1, 4, 5, 13, 15, 20, 21, 22, 23, 24, 26, 28, 30, 31)$

Alternative 5-var K-map

$F(A, B, C, D, E) = \sum m(0, 1, 4, 5, 13, 15, 20, 21, 22, 23, 24, 26, 28, 30, 31)$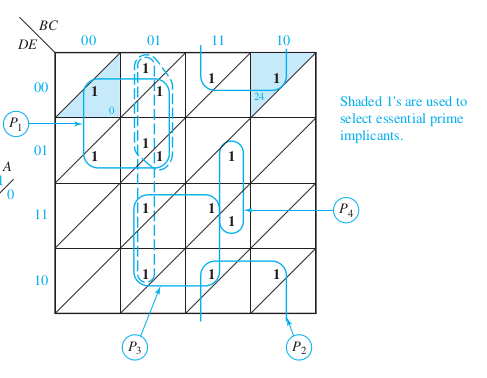

Roth's Fundamental of Logic Design

Minimum Cover: Ex 1

$f (x 1 , \dots , x 4 ) = \sum m(0, 2, 5, 6, 7, 8, 9, 13) + D(1, 12, 15)$

$P = \{ p_1 = 00*0, p_2 = 0*10, p_3 = 011*, p_4 = *00*, p_5 = **01, p_6 = 1*0*, p_7 = *1*1\}$

Minimum Cover: Ex 1

$f (x 1 , \dots , x 4 ) = \sum m(0, 2, 5, 6, 7, 8, 9, 13) + D(1, 12, 15)$

$P = \{ p_1 = 00*0, p_2 = 0*10, p_3 = 011*, p_4 = *00*, p_5 = **01, p_6 = 1*0*, p_7 = *1*1\}$

$f = \bx_1 x_3 \bx_4 + \bx_2 \bx_3 + x_2 x_4$

Minimum Cover: Ex 2

$f (xx1 , \dots, x_4 ) = \sum m(0, 3, 10, 15) + D(1, 2, 7, 8, 11, 14)$

$P = \{p_1 = 00**, p_2 = *0*0, p_3 = *01*, p_4 = **11, p_5 = 1*1*\}$

Minimum Cover: Ex 2

$f (xx1 , \dots, x_4 ) = \sum m(0, 3, 10, 15) + D(1, 2, 7, 8, 11, 14)$

$P = \{p_1 = 00**, p_2 = *0*0, p_3 = *01*, p_4 = **11, p_5 = 1*1*\}$

Including $p_3$

$C = \{ p_1 , p_3, p_4 \}$

Excluding $p_3$

$C = \{ p_1 , p_5 \}$

$f = \bx_1 \bx_2 + x_1 x_3$

Quine McCluskey algorithm

Find PIs

Start with a list of cubes (products) that represent the minterms where f = 1 or a don’t-care condition.
Arrange the minterms in groups of increasing number of ones in the binary representation.
Generate the prime implicants by successive pairwise comparisons of the cubes.

Find minimum cover

Derive a cover table which indicates the minterms where f = 1 that are covered by each prime implicant.
Include the essential prime implicants (if any) in the final cover and reduce the table by removing both these prime implicants and the covered minterms.
Use the concept of row and column dominance to reduce the cover table further. A dominated row is removed only if the cost of its prime implicant is greater than or equal to the cost of the dominating row’s prime implicant.
Repeat steps 3 and 4 until the cover table is either empty or no further reduction of the table is possible.
If the reduced cover table is not empty, then use the branching approach to determine the remaining prime implicants that should be included in a minimum cost cover.

K-map flowchart

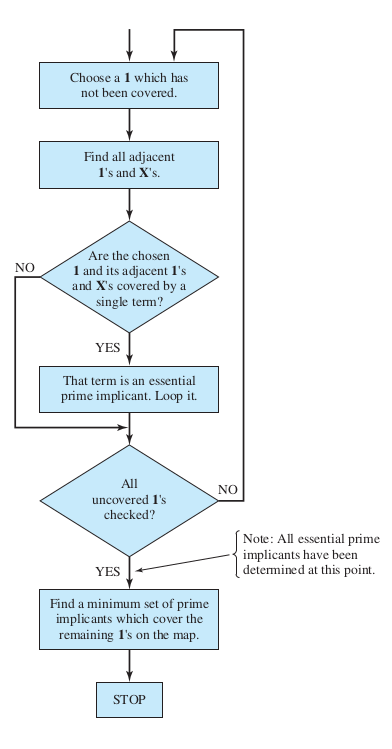
Roth's Fundamental of Logic Design

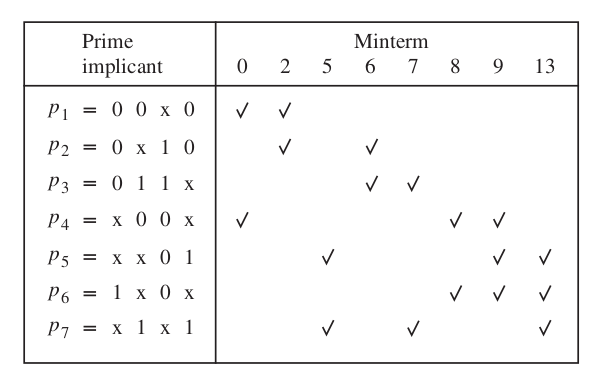
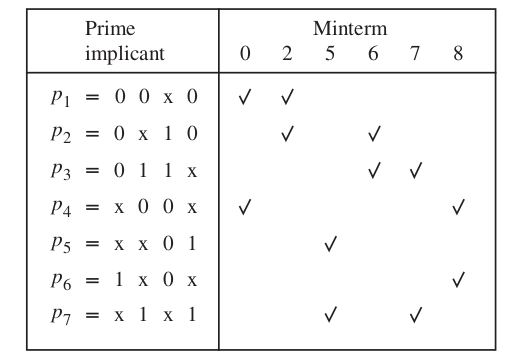
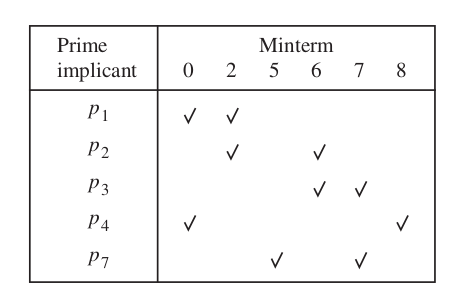
Petricks method

$P = \{ p_1 = 00*0, p_2 = 0*10, p_3 = 011*, p_4 = *00*, p_5 = **01, p_6 = 1*0*, p_7 = *1*1\}$

Petricks method

$P = \{ p_1 = 00*0, p_2 = 0*10, p_3 = 011*, p_4 = *00*, p_5 = **01, p_6 = 1*0*, p_7 = *1*1\}$

$\begin{align} &(p_1 + p_4)(p_1 + p_2)(p_5 + p_7)(p_2 + p_3)(p_3 + p_7)\underbrace{(p_4 + p_6)(p_4 + p_5 + p_6)}_{(p_4 + p_6)}(p_5 + p_6 + p_7) \\ &= (p_1 + p_4)(p_1 + p_2)(p_2 + p_3)(p_3 + p_7)(p_4 + p_6)\underbrace{(p_5 + p_7)(p_5 + p_6 + p_7)}_{(p_5 + p_7)} \\ &= (p_1 + p_4)(p_1 + p_2)(p_2 + p_3)(p_3 + p_7)(p_4 + p_6)(p_5 + p_7) \\ &= (p_1 + p_4p_2 + p_1 p_2)(p_2 p_7 +p_2 p_3 + p_3 p_7 + p_3)(p_4 p_5 + p_4 p_7 + p_6p_5 + p_6 p_7) \\ &= (p_1 + p_4p_2 + p_1 p_2)(p_2 p_7 +p_2 p_3 + p_3 p_7 + p_3)(p_4 p_5 + p_4 p_7 + p_6p_5 + p_6 p_7) \\ &= (p_1 + p_4p_2)(p_2 p_7 + p_3)(p_4 p_5 + p_4 p_7 + p_6p_5 + p_6 p_7) \\ &= (p_1 p_2 p_7 + p_1 p_3 + p_2 p_4 p_7 + p_2 p_3 p_4)(p_4 p_5 + p_4 p_7 + p_5 p_6 + p_6 p_7) \\ &= p_1 p_2 p_4 p_5 p_7 + p_1 p_2 p_4 p_7 + p_1 p_2 p_5 p_6 p_7 + p_1 p_2 p_6 p_7 \\&\qquad + p_1 p_3 p_4 p_5 + p_1 p_3 p_4 p_7 + p_1 p_3 p_5 p_6 + p_1 p_3 p_6 p_7 \\&\qquad + p_2 p_4 p_5 p_7 + \color{red}{p_2 p_4 p_7} + p_2 p_4 p_5 p_6 p_7 + p_2 p_4 p_6 p_7 \\&\qquad + p_2 p_3 p_4 p_5 + p_2 p_3 p_4 p_7 + p_2 p_3 p_4 p_5 p_6 + p_2 p_3 p_4 p_6 p_7 \end{align}$

$f = p_2 + p_4 + p_7 = \bx_1 x_2 \bx_4 + \bx_2 \bx_3 + x_2 x_4$

Multi output functions: Ex 1

$f_1$

		$\bar{x}_1$		$x_1$
		$\bar{x}_2$	$x_2$		$\bar{x}_2$
$\bar{x}_3$	$\bar{x}_4$	0	0	0	0
$\bar{x}_3$	$x_4$	0	1	1	0
$x_3$	$x_4$	0	1	1	0
$x_3$	$\bar{x}_4$	1	1	0	0

$f_2$

		$\bar{x}_1$		$x_1$
		$\bar{x}_2$	$x_2$		$\bar{x}_2$
$\bar{x}_3$	$\bar{x}_4$	0	0	0	0
$\bar{x}_3$	$x_4$	0	1	0	0
$x_3$	$x_4$	0	1	0	0
$x_3$	$\bar{x}_4$	1	1	0	0

$f_2$

		$\bar{x}_1$		$x_1$
		$\bar{x}_2$	$x_2$		$\bar{x}_2$
$\bar{x}_3$	$\bar{x}_4$	0	0	0	0
$\bar{x}_3$	$x_4$	0	0	1	1
$x_3$	$x_4$	0	0	1	0
$x_3$	$\bar{x}_4$	0	0	0	0

Multi output functions: Ex 2

$f_1$

		$\bar{x}_1$		$x_1$
		$\bar{x}_2$	$x_2$		$\bar{x}_2$
$\bar{x}_3$	$\bar{x}_4$	0	0	1	0
$\bar{x}_3$	$x_4$	0	0	1	0
$x_3$	$x_4$	0	0	1	1
$x_3$	$\bar{x}_4$	0	0	1	0

$f_2$

		$\bar{x}_1$		$x_1$
		$\bar{x}_2$	$x_2$		$\bar{x}_2$
$\bar{x}_3$	$\bar{x}_4$	0	0	1	0
$\bar{x}_3$	$x_4$	0	0	1	0
$x_3$	$x_4$	1	1	1	1
$x_3$	$\bar{x}_4$	0	0	0	0

$f_2$

		$\bar{x}_1$		$x_1$
		$\bar{x}_2$	$x_2$		$\bar{x}_2$
$\bar{x}_3$	$\bar{x}_4$	0	0	1	0
$\bar{x}_3$	$x_4$	1	1	1	0
$x_3$	$x_4$	0	0	1	0
$x_3$	$\bar{x}_4$	0	0	1	0

EPIs for Multi-output functions

For multiple output functions, we consider only those 1's for EPI that are not present in other fuction maps.

$f_1$

		$\bar{x}_1$		$x_1$
		$\bar{x}_2$	$x_2$		$\bar{x}_2$
$\bar{x}_3$	$\bar{x}_4$	0	0	0	0
$\bar{x}_3$	$x_4$	1	1	1	1
$x_3$	$x_4$	0	0	1	0
$x_3$	$\bar{x}_4$	0	0	0	0

$f_2$

		$\bar{x}_1$		$x_1$
		$\bar{x}_2$	$x_2$		$\bar{x}_2$
$\bar{x}_3$	$\bar{x}_4$	0	1	1	0
$\bar{x}_3$	$x_4$	0	0	0	0
$x_3$	$x_4$	0	0	1	0
$x_3$	$\bar{x}_4$	0	1	1	0

Thanks, Questions, Feedback?

https://vikasdhiman.info/ECE275-Sequential-Logic/

ECE 275: Finding minimal cover/Petrick's method

Announcments

Hw2 Prob 8: POS form

Alternative 5-var K-map

Alternative 5-var K-map

Minimum Cover: Ex 1

Minimum Cover: Ex 1

Minimum Cover: Ex 2

Minimum Cover: Ex 2

Including $p_3$

Excluding $p_3$

Quine McCluskey algorithm

Find PIs

Find minimum cover

K-map flowchart

Petricks method

Petricks method

Multi output functions: Ex 1

$f_1$

$f_2$

$f_2$

Multi output functions: Ex 2

$f_1$

$f_2$

$f_2$

EPIs for Multi-output functions

$f_1$

$f_2$

Thanks, Questions, Feedback?