ECE 275: Multi-level synthesis
Announcments
- Homework 4 has only four problems and is due on Oct 1st Friday by midnight.
- We will review material covered so far on Oct 4th, please email me topics that you want to be reviewed.
- Midterm is on Oct 6th, 9 AM in class. All problems will be variations of the homework problems.
Gates review
AND gate
\( f(x_1, x_2) = x_1 \cdot x_2 \)
\( f(x_1, x_2) = x_1 \cdot x_2 \)
OR gate
\( f_{\text{OR}}(x_1, x_2) = x_1 + x_2 \)
\( f_{\text{OR}}(x_1, x_2) = x_1 + x_2 \)
NOT gate
\( L_{\text{NOT}}(x_1) = \bar{x}_1 \)
\( L_{\text{NOT}}(x_1) = \bar{x}_1 \)
NAND gate
\( Q = \overline{x_1 \cdot x_2} \)
\( Q = \overline{x_1 \cdot x_2} \)
NOR gate
\( Q = \overline{x_1 + x_2} \)
\( Q = \overline{x_1 + x_2} \)
XOR gate
\( Q = \bx_1 x_2 + x_1 \bx_2 = x_1 \oplus x_2 \)
\( Q = \bx_1 x_2 + x_1 \bx_2 = x_1 \oplus x_2 \)
Approaches for Multi-level synthesis
- Factorization
- Functional decomposition
Functional decomposition Ex1
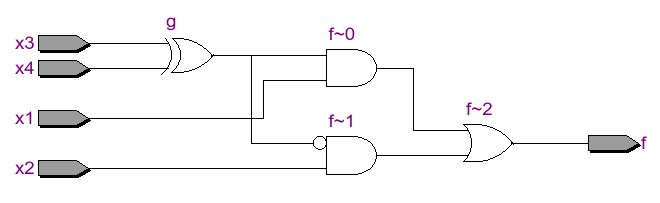
\[ f = \bx_1 x_2 x_3 + x_1 \bx_2 x_3 + \bx_1 \bx_2 x_4 + x_1 x_2 x_4 \]Functional decomposition Ex1
\[ f = \bx_1 x_2 x_3 + x_1 \bx_2 x_3 + \bx_1 \bx_2 x_4 + x_1 x_2 x_4 \]| \(\bar{x}_1\) | \(x_1 \) | ||||
|---|---|---|---|---|---|
| \(\bar{x}_2\) | \(x_2 \) | \(\bar{x}_2\) | |||
| \(\bar{x}_3\) | \(\bar{x}_4\) | 0 | 0 | 0 | 0 |
| \(x_4\) | 1 | 0 | 1 | 0 | |
| \(x_3\) | 1 | 1 | 1 | 1 | |
| \(\bar{x}_4\) | 0 | 1 | 0 | 1 | |
Functional decomposition Ex2
\[ f = \sum m(0, 6, 8, 14) \]| \(\bar{x}_1\) | \(x_1 \) | ||||
|---|---|---|---|---|---|
| \(\bar{x}_2\) | \(x_2 \) | \(\bar{x}_2\) | |||
| \(\bar{x}_3\) | \(\bar{x}_4\) | 1 | 0 | 0 | 1 |
| \(x_4\) | 0 | 0 | 0 | 0 | |
| \(x_3\) | 0 | 0 | 0 | 0 | |
| \(\bar{x}_4\) | 0 | 1 | 1 | 0 | |
Functional decomposition Ex3
| \(\bx_5 \) | |||||
|---|---|---|---|---|---|
| \(\bar{x}_1\) | \(x_1 \) | ||||
| \(\bar{x}_2\) | \(x_2 \) | \(\bar{x}_2\) | |||
| \(\bar{x}_3\) | \(\bar{x}_4\) | 1 | 0 | 0 | 0 |
| \(x_4\) | 0 | 1 | 1 | 1 | |
| \(x_3\) | 1 | 0 | 0 | 0 | |
| \(\bar{x}_4\) | 0 | 1 | 1 | 1 | |
| \(x_5 \) | |||||
|---|---|---|---|---|---|
| \(\bar{x}_1\) | \(x_1 \) | ||||
| \(\bar{x}_2\) | \(x_2 \) | \(\bar{x}_2\) | |||
| \(\bar{x}_3\) | \(\bar{x}_4\) | 0 | 0 | 0 | 0 |
| \(x_4\) | 1 | 1 | 1 | 1 | |
| \(x_3\) | 0 | 0 | 0 | 0 | |
| \(\bar{x}_4\) | 1 | 1 | 1 | 1 | |
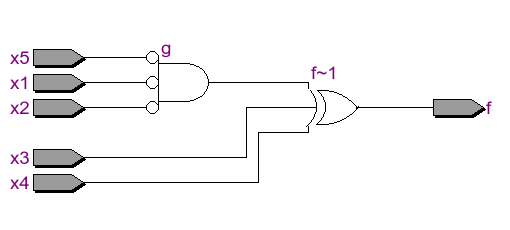
Functional decomposition Ex3
| \(\bx_5 \) | |||||
|---|---|---|---|---|---|
| \(\bar{x}_1\) | \(x_1 \) | ||||
| \(\bar{x}_2\) | \(x_2 \) | \(\bar{x}_2\) | |||
| \(\bar{x}_3\) | \(\bar{x}_4\) | 1 | 0 | 0 | 0 |
| \(x_4\) | 0 | 1 | 1 | 1 | |
| \(x_3\) | 1 | 0 | 0 | 0 | |
| \(\bar{x}_4\) | 0 | 1 | 1 | 1 | |
| \(x_5 \) | |||||
|---|---|---|---|---|---|
| \(\bar{x}_1\) | \(x_1 \) | ||||
| \(\bar{x}_2\) | \(x_2 \) | \(\bar{x}_2\) | |||
| \(\bar{x}_3\) | \(\bar{x}_4\) | 0 | 0 | 0 | 0 |
| \(x_4\) | 1 | 1 | 1 | 1 | |
| \(x_3\) | 0 | 0 | 0 | 0 | |
| \(\bar{x}_4\) | 1 | 1 | 1 | 1 | |
Functional decomposition Ex4
| \(\bA \) | |||||
|---|---|---|---|---|---|
| \(\bB\) | \(B \) | ||||
| \(\bC\) | \(C \) | \(\bC\) | |||
| \(\bD\) | \(\bE\) | 0 | 1 | 1 | 1 |
| \(E\) | 1 | 0 | 0 | 0 | |
| \(D\) | 0 | 1 | 1 | 1 | |
| \(\bE\) | 1 | 0 | 0 | 0 | |
| \(\bA \) | |||||
|---|---|---|---|---|---|
| \(\bB\) | \(B \) | ||||
| \(\bC\) | \(C \) | \(\bC\) | |||
| \(\bD\) | \(\bE\) | 1 | 0 | 0 | 0 |
| \(E\) | 0 | 1 | 0 | 0 | |
| \(D\) | 1 | 0 | 0 | 0 | |
| \(\bE\) | 0 | 1 | 0 | 0 | |
Thanks, Questions, Feedback?
https://vikasdhiman.info/ECE275-Sequential-Logic/