ECE 275: Building blocks
Multiplexers (MUX)
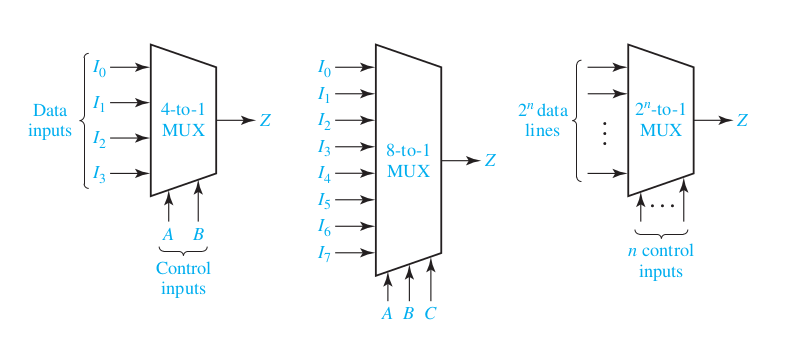
Three state buffers
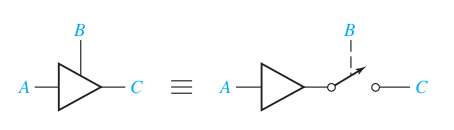
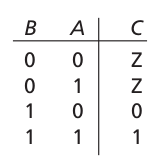
3-to-8 Decoders
ROM
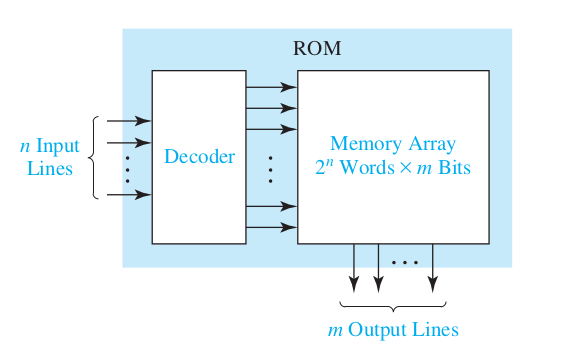
Encoder
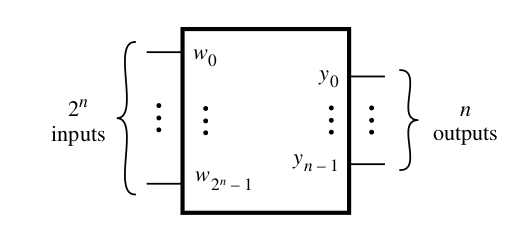
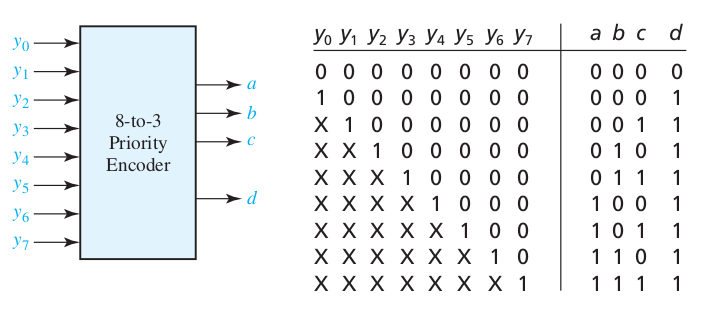
Priority Encoder
Circuits using Multiplexer
| \( w_1 \) | \( w_0 \) | \( f \) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Shannon's expansion theorem
\[ f(x_1, \dots, x_i, \dots, x_n) = x_i f(x_1, \dots, 1, \dots, x_n) + \bx_i f(x_1, \dots, 0, \dots, x_n) \]
\[ f(x_1, \dots, x_n) = x_i f_{x_i}(x_1, \dots, x_n) + \bx_i f_{\bx_i}(x_1, \dots, x_n) \]
Design a cicuit using 4:1 MUX
| \(\bar{w}_1\) | \(w_1 \) | ||||
|---|---|---|---|---|---|
| \(\bar{w}_2\) | \(w_2 \) | \(\bar{w}_2\) | |||
| \(\bar{w}_3\) | \(\bar{w}_4\) | 0 | 1 | 1 | 0 |
| \(w_4\) | 0 | 1 | 0 | 1 | |
| \(w_3\) | 1 | 1 | 0 | 1 | |
| \(\bar{w}_4\) | 1 | 1 | 1 | 0 | |
Design a cicuit using 4:1 MUX
| \(\bar{w}_1\) | \(w_1 \) | ||||
|---|---|---|---|---|---|
| \(\bar{w}_2\) | \(w_2 \) | \(\bar{w}_2\) | |||
| \(\bar{w}_3\) | \(\bar{w}_4\) | 0 | 1 | 1 | 0 |
| \(w_4\) | 0 | 1 | 0 | 1 | |
| \(w_3\) | 1 | 1 | 0 | 1 | |
| \(\bar{w}_4\) | 1 | 1 | 1 | 0 | |
Design using 3-to-8 Decoder
| Row | \( w_2 \) | \( w_1 \) | \( w_0 \) | \( f \) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 0 |
Thanks, Questions, Feedback?
https://vikasdhiman.info/ECE275-Sequential-Logic/