\[
\newcommand{\bx}{\bar{x}}
\newcommand{\by}{\bar{y}}
\newcommand{\bz}{\bar{z}}
\newcommand{\bA}{\bar{A}}
\newcommand{\bB}{\bar{B}}
\newcommand{\bC}{\bar{C}}
\newcommand{\bD}{\bar{D}}
\newcommand{\bE}{\bar{E}}
\]
ECE 275: State reduction
Announcemnts
- Midterm 2 postponed to Nov 15th instead of Nov 8th.
- HW 8 is posted is due next Wednesday (Nov 10th) at 9 AM before class.
Ex2: Parity Checker
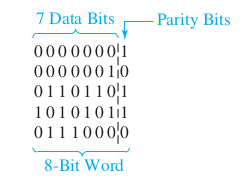
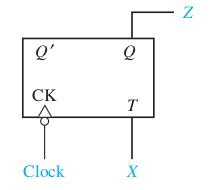
Ex2: Parity Checker using T flip-flops

Ex2: Parity Checker using J-K flip-flops

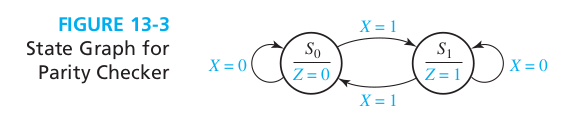
Ex2: Parity Checker

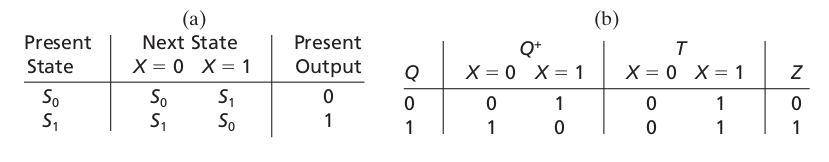
State reduction: Ex1
A sequential circuit has one input (X) and one output (Z). The circuit examines groups of four consecutive inputs and produces an output \( Z = 1 \) if the input sequence 0101 or 1001 occurs. The circuit resets after every four inputs. Find the Mealy state graph.State reduction: Ex1
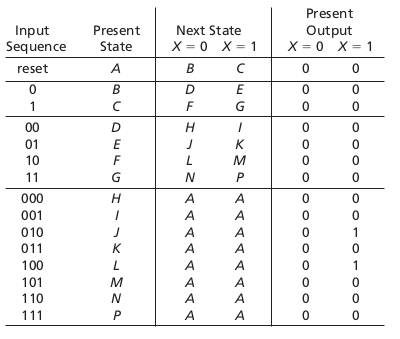
State reduction

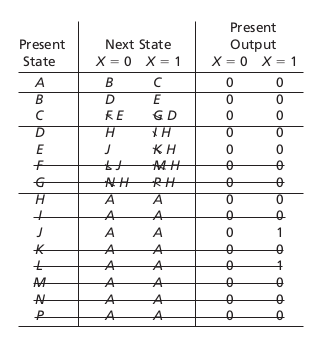
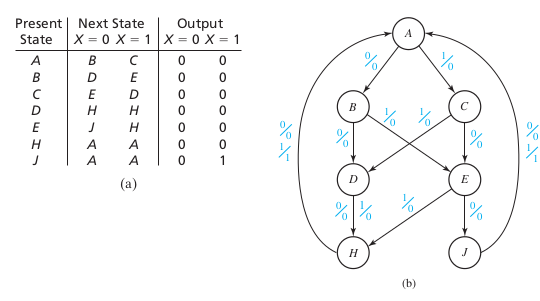
Equivalent states
Let \( N_1 \) and \( N_2 \) be sequential circuits (not necessarily different). Let \( \underline{X} \) represent a sequence of inputs of arbitrary length. Then state p in \( N_1 \) is equivalent to state q in \( N_2 \) iff \( \lambda_1(p, \underline{X} ) = \lambda_2 (q, \underline{X}) \) for every possible input sequence.Equivalent states
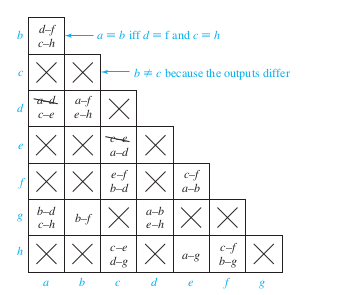
Two states p and q of a sequential circuit are equivalent iff for every single input X, the outputs are the same and the next states are equivalent, that is, \( \lambda(p, X) = \lambda(q, X) \) and \( \phi(p, X) = \phi(q, X) \).Implication tables: Ex2
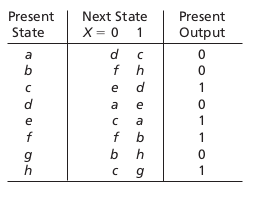
Implication tables

Thanks, Questions, Feedback?
https://vikasdhiman.info/ECE275-Sequential-Logic/